Theoretical Evaluation of Impact Characteristics of Wavy Graphene Sheets with Disclinations Formed by Origami and Kirigami
Abstract
:1. Introduction
2. Methods
2.1. Simulation Models
2.2. MD Analysis Conditions
2.3. Continuum Mechanics Method
3. Results and Discussion
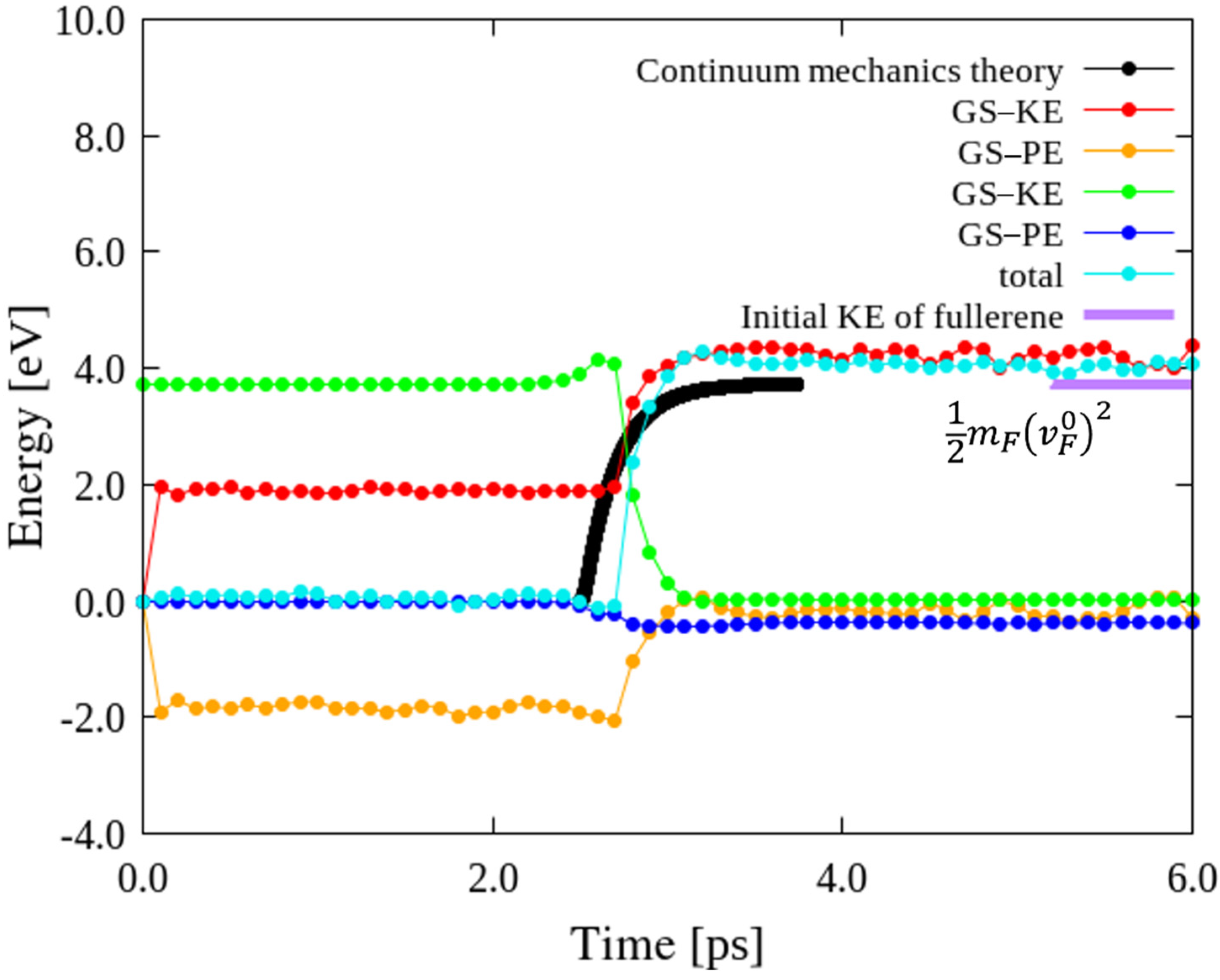
3.1. Comparison of Ideal GS Impact Tests via MD Simulation and Continuum Mechanics Method
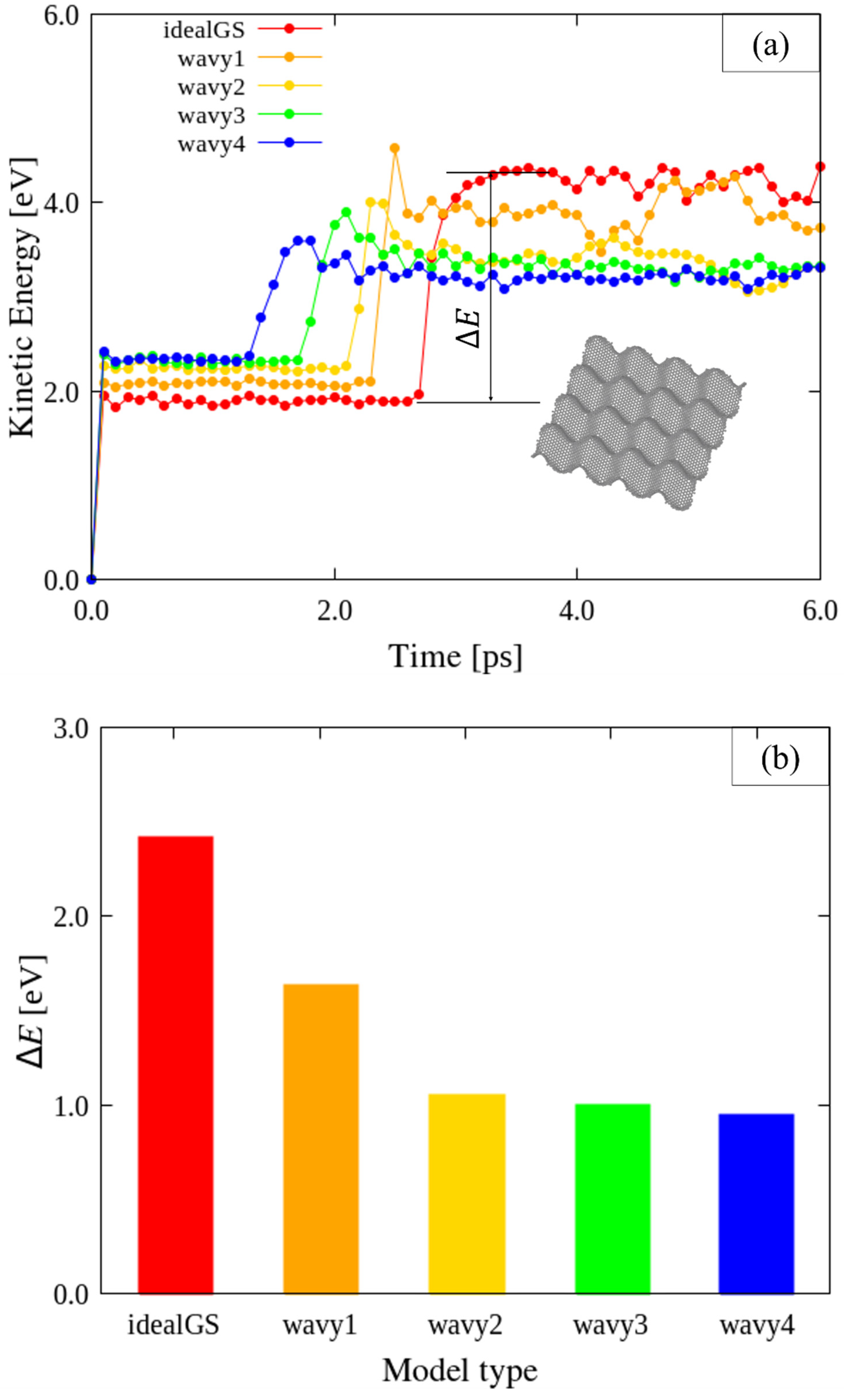
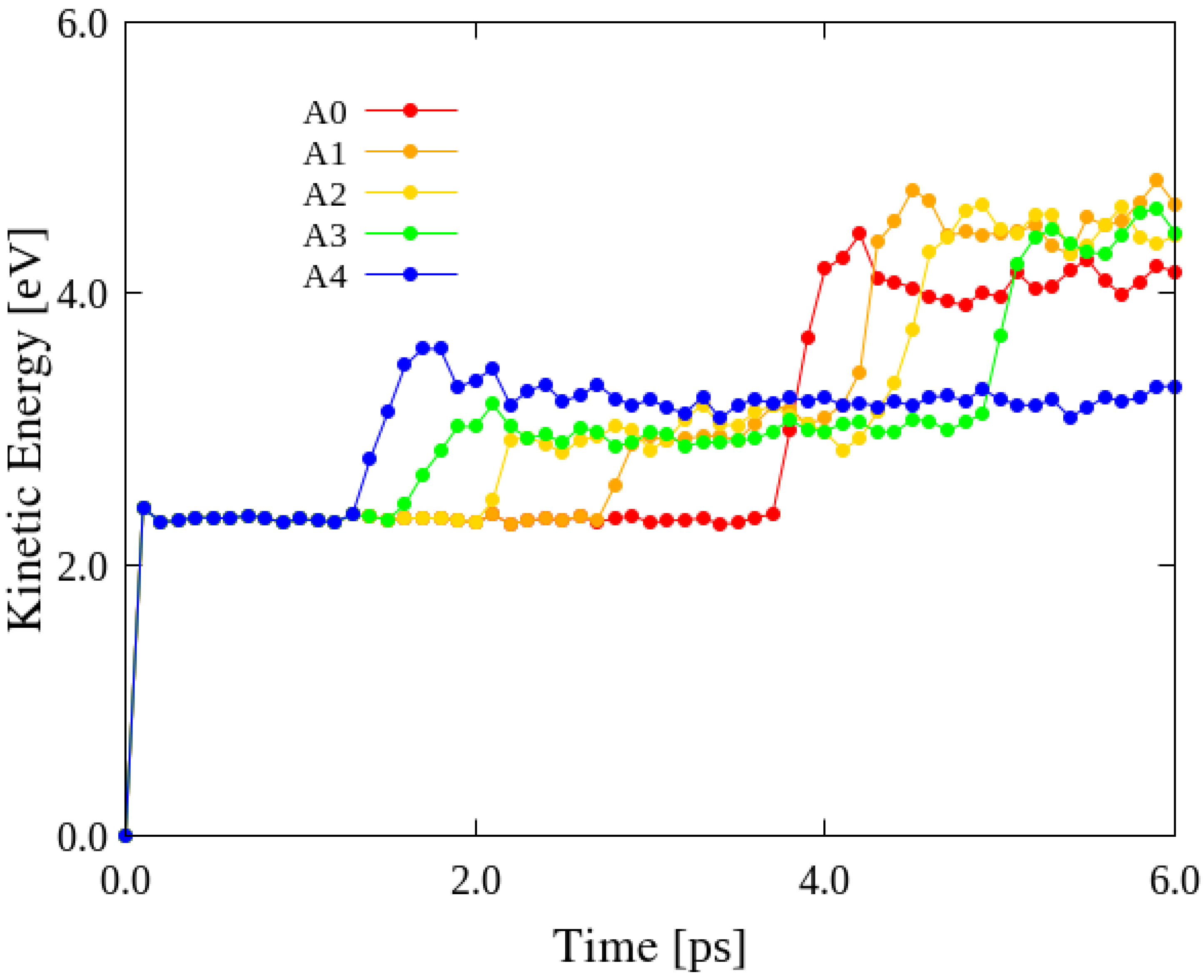
3.2. Effects of Disclination Density
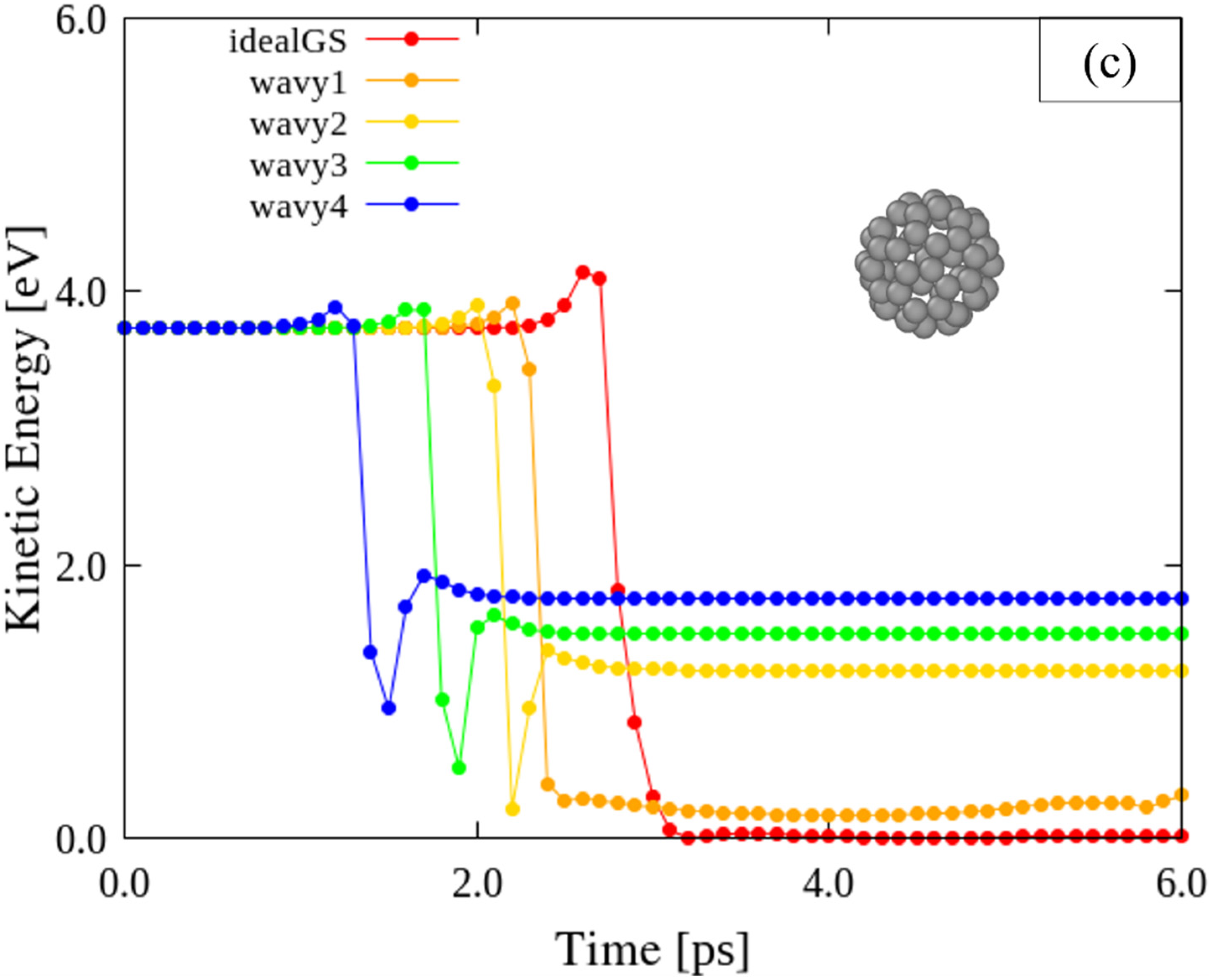
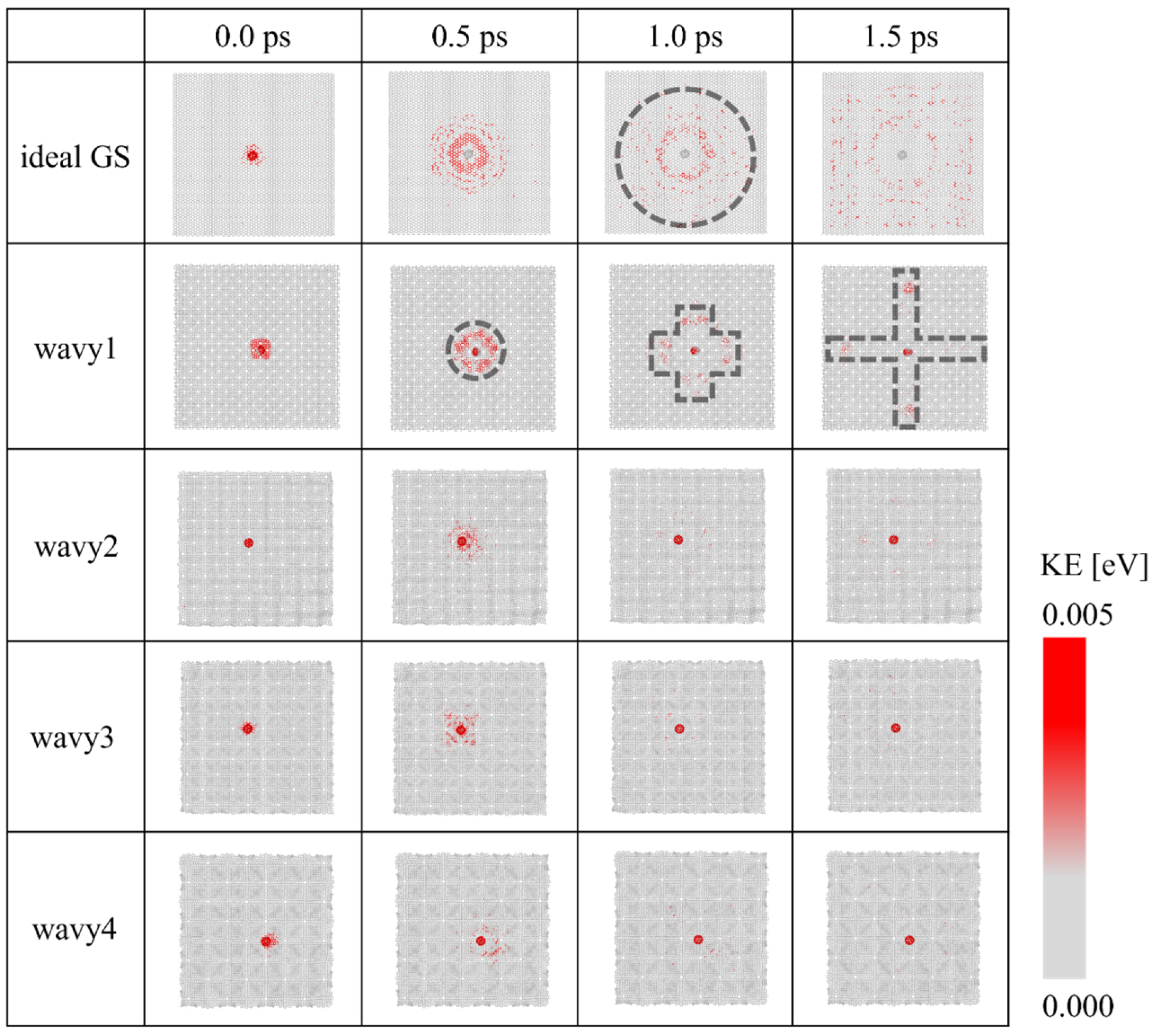
3.3. Distribution of KE
3.4. Effects of Impact Location
3.5. Effects of Impact Velocity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NEMS | nanoelectromechanical systems |
| GSs | graphene sheets |
| CNTs | carbon nanotubes |
| C60 | buckminsterfullerene |
| MD | molecular dynamics |
| KEs | kinetic energies |
| PEs | potential energies |
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.E.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Navarro, C.; Burghard, M.; Kern, K. Elastic properties of chemically derived single graphene sheets. Nano Lett. 2008, 8, 2045–2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb carbon: A review of graphene. Chem. Rev. 2010, 110, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Loya, P.E.; Lou, J.; Thomas, E.L. Dynamic mechanical behavior of multilayer graphene via supersonic projectile penetration. Science 2014, 346, 1092–1096. [Google Scholar] [CrossRef]
- Boland, C.S.; Khan, U.; Binions, M.; Barwich, S.; Boland, J.B.; Weaire, D.; Coleman, J.N. Graphene-coated polymer foams as tuneable impact sensors. Nanoscale 2018, 10, 5366–5375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, Y.; Zhang, Y.; Ademiloye, A.S.; Wu, Z. Molecular dynamics simulations of single-layer and rotated double-layer graphene sheets under a high velocity impact by fullerene. Comput. Mater. Sci. 2020, 182, 109798. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Sepahi-Boroujeni, A.; Sepahi-Boroujeni, S. Analytical and molecular dynamics studies on the impact loading of single-layered graphene sheet by fullerene. Appl. Surf. Sci. 2018, 437, 366–374. [Google Scholar] [CrossRef]
- Haque, B.Z.G.; Chowdhury, S.C.; Gillespie, J.W., Jr. Molecular simulations of stress wave propagation and perforation of graphene sheets under transverse impact. Carbon 2016, 102, 126–140. [Google Scholar] [CrossRef]
- Coluci, V.R.; Dantas, S.O.; Jorio, A.; Galvao, D.S. Mechanical properties of carbon nanotube networks by molecular mechanics and impact molecular dynamics calculations. Phys. Rev. B 2007, 75, 075417. [Google Scholar] [CrossRef]
- Seifoori, S.; Hajabdollahi, H. Impact behavior of single-layered graphene sheets based on analytical model and molecular dynamics simulation. Appl. Surf. Sci. 2015, 351, 565–572. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, S. Mechanisms of diverting out-of-plane impact to transverse response in plate structures. Int. J. Impact Eng. 2019, 133, 103346. [Google Scholar] [CrossRef]
- Seifoori, S.; Khoshgoftar, M.J. Impact and vibration response of multi-layered graphene sheets under different striker based on the analytical model and molecular dynamics. Superlattices Microstruct. 2019, 135, 106249. [Google Scholar] [CrossRef]
- Natsuki, T.; Ni, Q.Q. Theoretical analysis of transverse impact response in double layer graphene sheets. AIP Adv. 2016, 6, 015009. [Google Scholar] [CrossRef] [Green Version]
- Natsuki, T.; Natsuki, J. Transverse impact analysis of double-layered graphene sheets on an elastic foundation. Int. J. Eng. Sci. 2018, 124, 41–48. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, C.; Xu, T.; Sun, Y.; Liu, B.; Li, Y. An analytical model for deformation and damage of rectangular laminated glass under low-velocity impact. Compos. Struct. 2017, 176, 833–843. [Google Scholar] [CrossRef]
- Warner, J.H.; Margine, E.R.; Mukai, M.; Robertson, A.W.; Giustino, F.; Kirkland, A.I. Dislocation-driven deformations in graphene. Science 2012, 337, 209–212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Romanov, A.E.; Rozhkov, M.A.; Kolesnikova, A.L. Disclinations in polycrystalline graphene and pseudo-graphenes. Review. Lett. Mater. 2018, 8, 384–400. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.; Gao, H. Defects controlled wrinkling and topological design in graphene. J. Mech. Phys. Solids 2014, 67, 2–13. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Li, X.; Gao, H. Designing graphene structures with controlled distributions of topological defects: A case study of toughness enhancement in graphene ruga. Extrem. Mech. Lett. 2014, 1, 3–8. [Google Scholar] [CrossRef]
- Lee, G.D.; Wang, C.Z.; Yoon, E.; Hwang, N.M.; Kim, D.Y.; Ho, K.M. Diffusion, coalescence, and reconstruction of vacancy defects in graphene layers. Phys. Rev. Lett. 2005, 95, 205501. [Google Scholar] [CrossRef] [PubMed]
- Yazyev, O.V.; Chen, Y.P. Polycrystalline graphene and other two-dimensional materials. Nat. Nanotechnol. 2014, 9, 755–767. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Sun, Y.; Liu, J.Z.; Liu, Y. Mechanical properties of wrinkled graphene generated by topological defects. Carbon 2016, 108, 204–214. [Google Scholar] [CrossRef]
- Qin, H.; Sun, Y.; Liu, J.Z.; Li, M.; Liu, Y. Negative Poisson’s ratio in rippled graphene. Nanoscale 2017, 9, 4135–4142. [Google Scholar] [CrossRef]
- Shi, J.X.; Ohmura, K.; Shimoda, M.; Lei, X.W. A consistent methodology for optimal shape design of graphene sheets to maximize their fundamental frequencies considering topological defects. J. Mech. Phys. Solids 2018, 116, 117–134. [Google Scholar] [CrossRef]
- Chu, L.; Shi, J.; Cursi, E.S. The Fingerprints of resonant frequency for atomic vacancy defect identification in graphene. Nanomaterials 2021, 11, 3451. [Google Scholar] [CrossRef]
- Lei, X.W.; Nakatani, A.; Doi, Y.; Matsunaga, S. Bifurcation analysis of periodic kirigami structure with out-plane deformation. J. Soc. Mater. Sci. 2018, 67, 202–207. [Google Scholar] [CrossRef] [Green Version]
- Lei, X.W.; Bando, K.; Shi, J.X. Vibration Control of diamond nanothreads by lattice defect introduction for application in nanomechanical sensors. Nanomaterials 2021, 11, 2241. [Google Scholar] [CrossRef]
- Ni, B.; Zhang, T.; Li, J.; Li, X.; Gao, H. Topological design of graphene. In Handbook of Graphene; Stauber, T., Ed.; Scrivener: New York, NY, USA, 2019; Volume 2, pp. 1–44. [Google Scholar]
- Zhong, L.; Gao, H.; Li, X. Atomistic simulations of the tensile behavior of graphene fibers. Extrem. Mech. Lett. 2020, 37, 100699. [Google Scholar] [CrossRef]
- Lei, X.-W.; Nakatani, A. Local equilibrium configurations and minimum energy path of carbon nanotubes with Stone-Wales defects and their related pentagon-heptagon lattice defects. Comput. Mater. Sci. 2017, 133, 194–199. [Google Scholar] [CrossRef]
- Nelson, D.R. Defects and Geometry in Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Hirsch, P.B.; Howie, A.; Nicholson, R.B.; Pashley, D.W.; Whelan, M.J. Electron Microscopy of Thin Crystals; Butterworths: London, UK, 1965. [Google Scholar]
- Murayama, M.; Howe, J.M.; Hidaka, H.; Takaki, S. Atomic-level observation of disclination dipoles in mechanically milled, nanocrystalline Fe. Science 2002, 295, 2433–2435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krishnan, A.; Dujardin, E.; Treacy, M.M.J.; Hugdahl, J.; Lynum, S.; Ebbesen, T.W. Graphitic cones and the nucleation of curved carbon surfaces. Nature 1997, 388, 451–454. [Google Scholar] [CrossRef]
- Galligan, J.M. Disclinations in folded structures and geological strata. Nature 1972, 240, 144–145. [Google Scholar] [CrossRef]
- Hage, F.S.; Kepaptsoglou, D.M.; Seabourne, C.R.; Ramasse, Q.M.; Scott, A.J.; Prytz, Ø.; Gunnæs, A.E.; Helgesen, G. Dielectric response of pentagonal defects in multilayer graphene nano-cones. Nanoscale 2014, 6, 1833–1839. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Hebard, A.F. Buckminsterfullerene. Annu. Rev. Mater. Sci. 1993, 23, 159–191. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, X.L.; Zhang, Y.Y.; Wang, D.; Bao, D.L.; Que, Y.; Xiao, W.; Du, S.; Ouyang, M.; Pantelides, S.T.; et al. Atomically precise, custom-design origami graphene nanostructures. Science 2019, 365, 1036–1040. [Google Scholar] [CrossRef] [Green Version]
- Miura, K. The science of Miura-Ori: A review. In Origami 4, 1st ed.; Lang, R.J., Peters, A.K., Eds.; CRC Press: Boca Raton, FL, USA, 2009; pp. 87–99. [Google Scholar]
- Hosseini-Hashemi, S.; Sepahi-Boroujeni, A. Elastic impact response of a nonlocal rectangular plate. Int. J. Solids Struct. 2017, 109, 93–100. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Hertz, H. Miscellaneous Papers; Macmillan: London, UK, 1896. [Google Scholar]

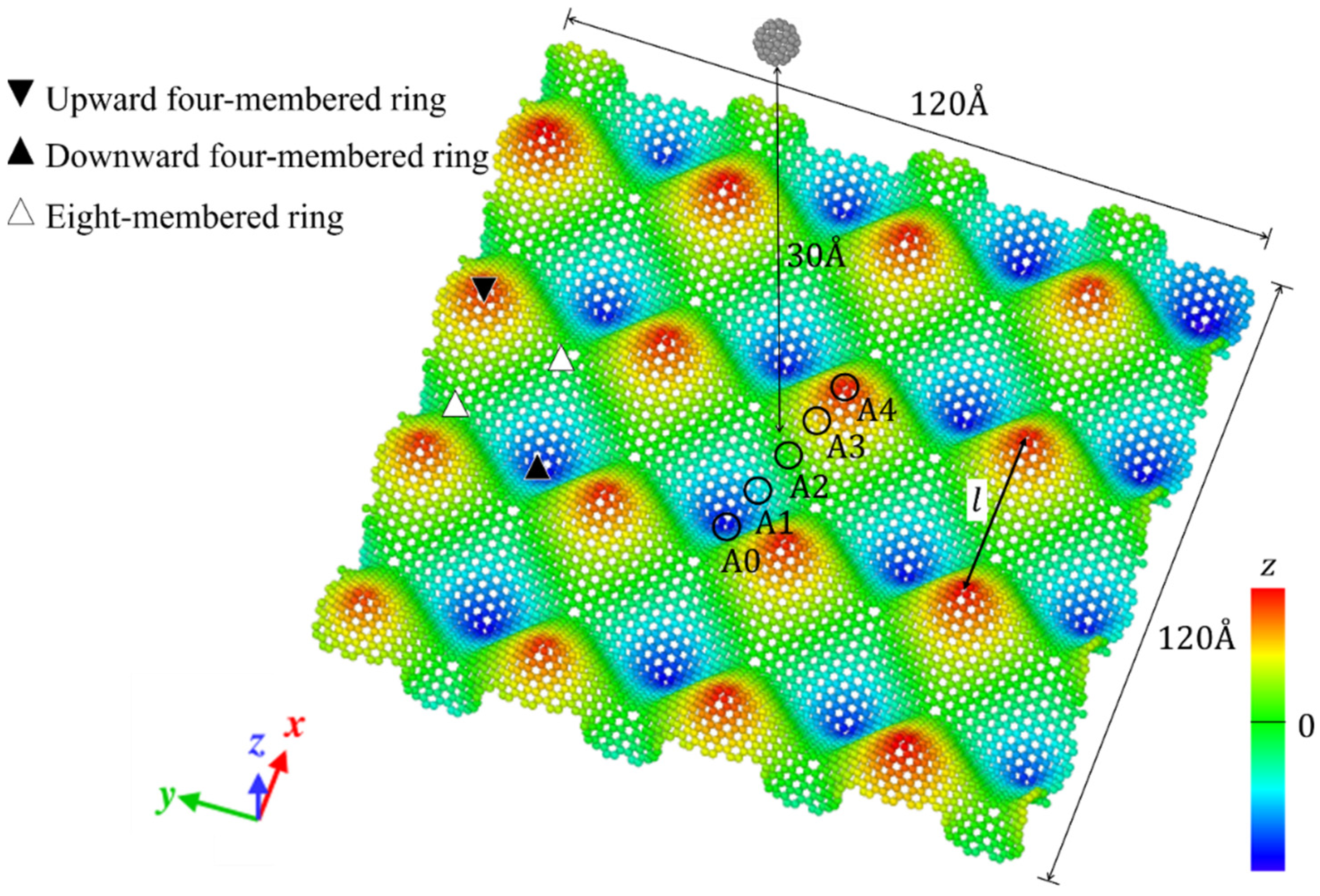

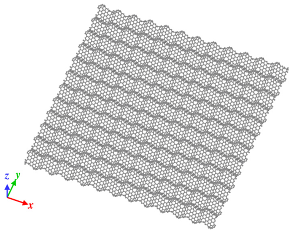 Model of wavy1 GS, l is 11.42 Å. Disclination density is 31.30 × 10−3/Å2. | 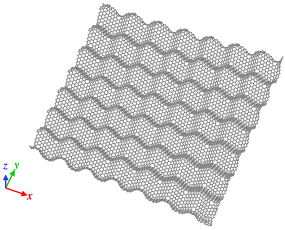 Model of wavy2 GS, l is 18.06 Å. Disclination density is 11.40 × 10−3/Å2. |
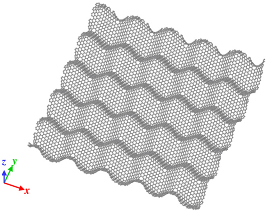 Model of wavy3 GS, l is 25.38 Å. Disclination density is 6.29 × 10−3/Å2. | 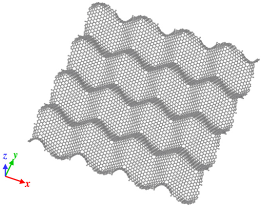 Model of wavy4 GS, l is 31.79 Å. Disclination density is 3.96 × 10−3/Å2. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomioka, Y.; Natsuki, T.; Shi, J.-X.; Lei, X.-W. Theoretical Evaluation of Impact Characteristics of Wavy Graphene Sheets with Disclinations Formed by Origami and Kirigami. Nanomaterials 2022, 12, 436. https://doi.org/10.3390/nano12030436
Tomioka Y, Natsuki T, Shi J-X, Lei X-W. Theoretical Evaluation of Impact Characteristics of Wavy Graphene Sheets with Disclinations Formed by Origami and Kirigami. Nanomaterials. 2022; 12(3):436. https://doi.org/10.3390/nano12030436
Chicago/Turabian StyleTomioka, Yoshitada, Toshiaki Natsuki, Jin-Xing Shi, and Xiao-Wen Lei. 2022. "Theoretical Evaluation of Impact Characteristics of Wavy Graphene Sheets with Disclinations Formed by Origami and Kirigami" Nanomaterials 12, no. 3: 436. https://doi.org/10.3390/nano12030436
APA StyleTomioka, Y., Natsuki, T., Shi, J.-X., & Lei, X.-W. (2022). Theoretical Evaluation of Impact Characteristics of Wavy Graphene Sheets with Disclinations Formed by Origami and Kirigami. Nanomaterials, 12(3), 436. https://doi.org/10.3390/nano12030436







